ALGORITMO DE PRIM
El algoritmo de Prim es un algoritmo perteneciente a la teoría de los grafos para encontrar un árbol de recorrido mínimo en un grafo conexo, no dirigido y cuyas aristas están etiquetadas.
En otras palabras, el algoritmo encuentra un subconjunto de aristas que forman un árbol con todos los vértices, donde el peso total de todas las aristas en el árbol es el mínimo posible. Si el grafo no es conexo, entonces el algoritmo encontrará el árbol recubridor mínimo para uno de los componentes conexos que forman dicho grafo no conexo.Elementos del algoritmo de Prim
Conjunto de candidatos: Vértices del grafo.
Función de selección: El vértice u aún no seleccionado que se conecte mediante la arista de menor peso a un vértice v del conjunto de vértices seleccionados.
Función de factibilidad:
El conjunto de aristas no contiene ningún ciclo.
Criterio que define lo que es una solución: n Criterio que define lo que es una solución: n-1 aristas.
El conjunto de aristas ( El conjunto de aristas (u,v) conecta todos los v ) conecta todos los vértices. Función objetivo: Suma de los costes de las aristas
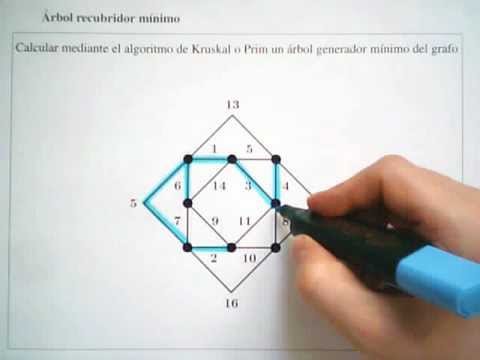
Ejemplo
Optimalidad del algoritmo de Prim Teorema:
Sean T un AGM de G=(V,A), S T un subarbol de T y (u,v) la arista de menor peso conectando los vertices de S con los de V-A. Entonces, (u,v) T.
Demostracion:
El teorema anterior se puede demostrar facilmente si tenemos en cuenta que un AGM tiene subestructuras optimales.
Optimalidad del algoritmo de Prim
Teorema: Sea T un AGM y (u,v) una arista de T. Si T y T son los dos arboles que se obtienen al eliminar la arista (u,v) de T, entonces T1 es un AGM de G =(V ,A ), y T es un AGM de G = (V ,A )
Demostración:
Por reduccion al absurdo: Si tenemos en cuenta que peso(T) = peso(u,v) + peso(T1) + peso(T2), no puede haber arboles generadores minimales mejores que T1 o T2, pues si los hubiese T no seria optimo.
Video algoritmo PRIM

No hay comentarios.:
Publicar un comentario