MATRIZ DISPERSA

¿QUE ES UNA MATRIZ DISPERSA? 

La matriz dispersa contiene formatos de almacenamiento en memoria, el objetivo es poder utilizar menos memoria de la que normalmente consume un equipo para el procesamiento de información.   

¿Cómo Inicio?

Inicialmente fue utilizada en la computación científica, especialmente en la optimización a gran escala de análisis estructural y de circuitos.
Igualmente fue aplicada en la teoría de grafos, teoría de redes, métodos  

Siempre buscando el mejor método para el menor consumo de memoria.  

TIPOS DE FORMATOS  

Los formatos que se representaran a continuación, mostraran las diferentes formas de como han tratado de implementar este tipo de matrices en equipos de computo.  

Lista Enlazada  

Es una estructura matriz donde se almacenan ceros (NULL) y unos (1), y la idea es crear una lista a partir de los elementos no vacíos.  

Ejemplo:  

 

 Formato Coordenado 

El formato coordenado es un avance frente a la lista enlazada ya que este tipo de formato se manejan con tres arreglos y el procesamiento de información es mejor. 

 Donde v = datos no nulos, i= fila donde se encuentra el dato y v= columna donde se encuentra el dato. 

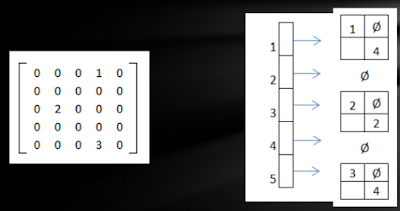
Lista Enlazada Por Fila 

Estos se reagrupan por fila por lo tanto, se tendrá una lista enlazada por cada fila matriz.  

Formato Comprimido Por Filas 

Conocido como CSR(Compressed Sparse Row), mas que todo utilizado en aplicaciones practicas, manejan los mismos tres vectores pero con una única diferencia:   

 El vector i almacenara la posición en donde empieza una nueva fila en el vector j. 

Formato Comprimido Por Columnas 

Conocido como CSC(Compressed Sparse Column), manejan los mismos tres vectores pero con una única diferencia:  

El vector j almacenara la posición en donde empieza  una nueva columna en el vector i.  

Bibliografía

www.imagui.com/a/munequito-blanco-3d-cgKbGGKxo
www.redalyc.org/articulo.oa?id=84927487025
www.youtube.com/watch?v=kzJ9Ux2xwSI